Dynamik des Antriebsstranges

Um eine optimale Regelung des Antriebsschlupfs realisieren zu können, muss bekannt sein, wie sich die Regelstrecke verhält. Dies kann sowohl durch Modellbildung, als auch durch experimentelle Streckencharakterisierung erreicht werden. Wir haben uns für letztere Variante entschieden.

Sprungfunktion=Volllast

Eine übliche Methode zur Streckencharakterisierung ist, einen Sprung des Stellsignals auf den Eingang zu geben. Im Falle eines Antriebsstranges heißt das: Volllast.

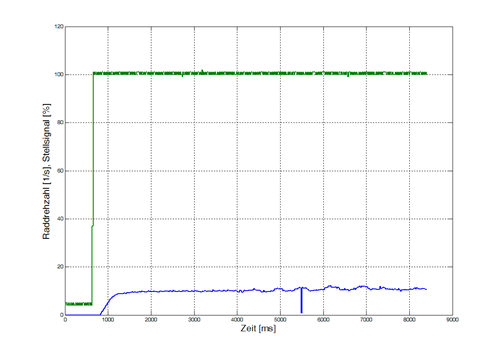
Sprung-Stellsignal

In grün dargestellt ist die Stellgröße Fahrpedal, wobei 0%=kein Gas und 100%=Vollgas bedeutet. Die blaue Kurve ist die Antwort des Fahrzeugs, nämlich die Raddrehzahl der Hinterräder. Zur empirischen Modellbildung empfiehlt es sich, eine vereinfachte Übertragungsfunktion zu parametrieren. In diesem Fall entspricht die Systemantwort in etwa einer PT2-Funktion. Das P bedeutet, dass es proportional auf eine Änderung reagiert, das T2, dass es zwei Zeitverzögerungen gibt.

Zeitprozentwertmethode

Zur Bestimmung der 3 Faktoren wurde die Zeitprozentwertmethode nach Ormanns genutzt. Diese ermöglicht, ein System 2. Ordnung mit einer gewissen Totzeit zu parametrieren.

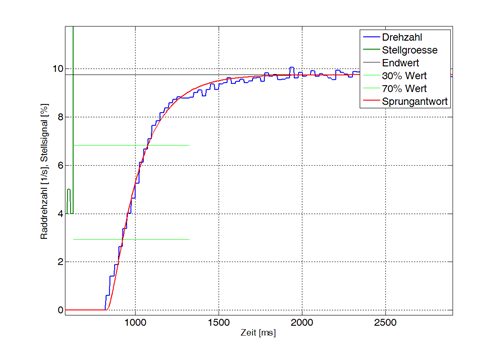
Zeitprozentwertmethode

In rot dargestellt die die ermittelte PT2-Übertragungsfunktion, welche das Verhalten des dynamischen Systems (Antriebsstrang samt Elektromotor) widerspiegelt. Die zwei Zeitkonstanten sind auf die elektrische Maschine und die mechanischen Massenträgheiten zurück zu führen. Wie man erkennen kann, gibt es eine erhebliche Verzugszeit (Totzeit), zwischen Betätigung des Gaspedals und Drehzahlreaktion der Räder.

Übertragungsfunktion

Die Übertragungsfunktion mit den Zeitkonstanten T₁ und T₂ sowie der Totzeit T_t ist:

$G(s)=\cfrac{0.092}{(1+s\cdot 0.113)(1+s\cdot 0.073)}\cdot e^{-0.197 \cdot s}$

Diese beschreibt die träge Reaktion der Raddrehzahlen auf die sprungartige Vorgabe einer Drehzahländerung durch das Fahrpedal. Darin enthalten sind die elektrischen Trägheiten (kleinere Zeitkonstante T₂) sowie die mechanischen Trägheiten (größere Zeitkonstante T₁). Die Totzeit kann sowohl vom Spiel des Ausgleichsgetriebes oder von Berechnungen des Drehzahlstellers für den Plettenberg Dinator Elektromotor kommen.

Matlab m-File

Das Matlab m-File zur Berechnung der Zeitkonstanten einer PT2-Tt-Sprungantwort aus Messwerten mittels der Zeitprozentwertmethode ist nachfolgend dargestellt.

% Ermittlung der Zeitkonstanten nach
% Zeitprozentwertmethode (Verfahren
% von ORMANNS), siehe http://goo.gl/BvWVx
%
% Voraussetzung:
% Zeitvektor im Workspace als “t”
% Messwert im Workspace als “messwert”

% Abfrage nach Sprung
    sprungmaximalwert=input('Welcher Wert wird als Stellgröße erreicht');

% Abfrage nach stationärem Endwert
    endwert=input('stationärer Endwert?');
    ab=input('Ab welcher Zeit wird der stationäre Endwert erreicht? [ms] ');
    index_ab = find(t>ab, 1);
    bis=input('Bis? [ms] ');
    index_bis = find(t>bis, 1);
    endwert = mean(messwert(index_ab:index_bis));

% Verstärkung
    K = endwert/sprungmaximalwert;

% Parameter erfassen
    sprung = input('Bei welcher Zeit wird der Sprung gegeben? [ms] ');
    reaktion = input('Wann reagiert das System? [ms] ');
    Tt = reaktion - sprung;

% 30% & 70% Wert ermitteln
    t30 = input('Zeitpunkt, zu dem 30% erreicht sind? ');
    t30 = t30 - Tt - sprung;
    t70 = input('Zeitpunkt, zu dem 70% erreicht sind? ');
    t70 = t70 - Tt - sprung;

    if t30/t70 > 0.45
        warndlg('Das Verhältnis aus t30 und t70 Zeit ist kritisch','Hinweis')
        disp('Empfehlungen für Ersatztotzeit:')
        disp([num2str(1.42*t30-0.92*t70) ' < Tt < ' num2str(1.82*t30-0.82*t70)]);
        disp(['statt der eigentlichen' num2str(Tt) 'ms']);
        return
    elseif t30/t70 < 0.296
        disp('Das Verfahren kann für diese Sprungantwort nicht angewendet werden!')
        return
    end

% Hilfswerte berechnen
    tau = 2*(1+t30/t70)*sqrt(0.45-t30/t70);
    rho = 1.2+0.1*(tau^2-0.2)*(tau^2-0.9);

% Zeitkonstanten berechnen
    clc
    T1 = t70/(2*rho)*(1+tau)
    T2 = t70/(2*rho)*(1-tau)

iSuPIa